Formula For Measuring Volume In Chemistry

The ideal gas law can be used to calculate the volume of gaseous products or reactants as needed. A gas collected in such a way is not pure, however, but contains a significant amount of water vapor. The measured pressure must therefore be corrected for the vapor pressure of water, which depends strongly on the temperature.

Volume is the quantification of the three-dimensional space a substance occupies. By convention, the volume of a container is typically its capacity, and how much fluid it is able to hold, rather than the amount of space that the actual container displaces. Volumes of many shapes can be calculated by using well-defined formulas. In some cases, more complicated shapes can be broken down into simpler aggregate shapes, and the sum of their volumes is used to determine total volume.

The volumes of other even more complicated shapes can be calculated using integral calculus if a formula exists for the shape's boundary. Beyond this, shapes that cannot be described by known equations can be estimated using mathematical methods, such as the finite element method. Alternatively, if the density of a substance is known, and is uniform, the volume can be calculated using its weight. This calculator computes volumes for some of the most common simple shapes.

Volume is an amount of space, in three dimensions, that a sample of matter occupies. The number and the phase of the molecules in the sample primarily determine the volume of a substance. Volume will be measured in many ways in this course, but the units are usually milliliters or cubic centimeters .

Methods for determining or delivering precise volumes include volumetric pipets and pycnometers; less precise methods include burets, graduated cylinders, and graduated pipets. To measure the density of a sample of material, both the mass and volume of the sample must be determined. For both solids and liquids, a balance can be used to measure mass; however, methods for determining volume are different for solids and liquids.

As liquids can flow and take the shapes of their containers, glassware such as a graduated cylinder or volumetric flask can be used to measure the volume of a liquid. The volume of an irregularly-shaped solid can be measured by submersion in a liquid — the difference in volume caused by addition of the solid is equal to the volume of the solid. A disadvantage of describing formulas as w/v (%) is that the description says nothing about the actual concentration of molecules in solution. What if we want equal amounts of two chemicals to be mixed together, so that for each molecule of substance #1 there is a single molecule of substance #2? The same amount in grams will likely not contain the same number of molecules of each substance. For example, you may work with a chemical that can be in one of several forms of hydration.

Calcium chloride can be purchased as a dry chemical in anhydrous form, so that what you weigh out is nearly all pure calcium chloride. On the other hand you may have a stock of dry chemical that is hydrated with seven water molecules per molecule of calcium chloride. The same mass of this chemical will contain fewer molecules of calcium chloride. As long as the molecular weight is known, we can describe a solution in the form of moles per liter, or simply molar .

For example, the space that a substance or 3D shape occupies or contains. Volume is often quantified numerically using the SI derived unit, the cubic metre. Volumes of some simple shapes, such as regular, straight-edged, and circular shapes can be easily calculated using arithmetic formulas. Volumes of complicated shapes can be calculated with integral calculus if a formula exists for the shape's boundary.

One-dimensional figures and two-dimensional shapes are assigned zero volume in the three-dimensional space. It is important to note that the molarity is defined as moles of solute per liter of solution, not moles of solute per liter of solvent. To get around this problem chemists commonly make up their solutions in volumetric flasks. These are flasks that have a long neck with an etched line indicating the volume.

The solute is added to the flask first and then water is added until the solution reaches the mark. The flasks have very good calibration so volumes are commonly known to at least four significant figures. To determine the density of an irregular solid in pellet form, add approximately 40 mL of water to a clean and dry 100-mL graduated cylinder.

Place the cylinder on an analytical balance and tare. Add approximately 10 pellets, and record the new volume after the addition. The mass is only the pellets, as the rest have been tared. Make at least two additional sets of mass and volume measurements to calculate an average value of the density.

The density for zinc was measured for three different samples. Note that, since the measurements were made in a graduated cylinder, which is less precise than a volumetric flask, the density has lower degree of precision. Because gases fill their containers, their volume is the same as the internal volume of the container. Liquids are commonly measured using containers, where the volume is marked or else is the internal shape of the container.

Examples of instruments used to measure liquid volume include measuring cups, graduated cylinders, flasks, and beakers. There are formulas for calculating the volume of regular solid shapes. Another method of determining the volume of a solid is to measure how much liquid it displaces. Of a substance is the ratio of the mass of a sample of the substance to its volume. The SI unit for density is the kilogram per cubic meter (kg/m3). Although there are exceptions, most liquids and solids have densities that range from about 0.7 g/cm3 to 19 g/cm3 .

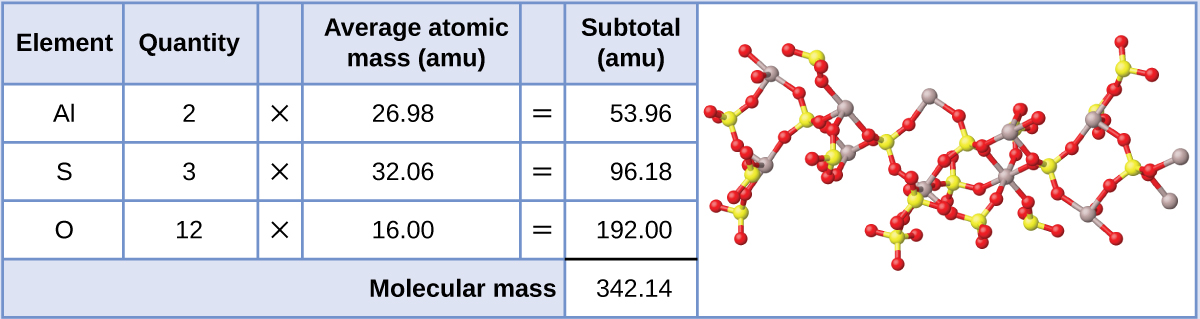
Table 1.4 shows the densities of some common substances. Table \(\PageIndex\) shows the densities of some common substances. As with w/v solutions, we weigh out a specific amount of chemical when making a molar solution. Unlike w/v solutions, the amount to weigh depends on the molecular weight (m.w.) of the substance in grams per mole (g/mol).

In order to calculate the desired mass of solute you will need to know the formula weight. Formula weights are usually printed on the label and identified by the abbreviation f.w. Formula weight is the mass of material in grams that contains one mole of substance, and may include inert materials and/or the mass of water molecules in the case of hydrated compounds.

For pure compounds the formula weight is the molecular weight of the substance and may be identified as such. Volume definition and formulas for common shapes.Volume is defined as the three-dimensional space occupied by matter or enclosed by a surface. The SI unit of volume is the cubic meter , but many units exist.

Other volume units include the liter , cubic centimeter , fluid ounce , pint , quart , gallon , teaspoon , and tablespoon . Explain to students that learning to measure volumes takes practice. Today they will practice measuring different liquids.

They will use a container called a graduated cylinder to measure liquids. Graduated cylinders have numbers on the side that help you determine the volume. Volume is measured in units called liters or fractions of liters called milliliters . Students need to follow the directions on the lab sheet carefully. Remind them that you will be checking how they measure as you move about the room. Perhaps the easiest way to describe a solution is in terms of weight-in-weight (w/w).

The weight of the solute relative to the weight of the final solution is described as a percentage. For example, suppose you have a dye that is soluble in alcohol. Rather than write the instructions, "take 3 grams dye and mix with 97 grams absolute alcohol," you can describe the solutions simply as 3% dye in absolute alcohol.

The formula applies to any volume of solution that might be required. Three grams dye plus 97 grams alcohol will have final weight of 100 grams, so the dye winds up being 3% of the final weight. Note that the final weight is not necessarily equal to the final volume.

Aqueous weight-in-weight solutions are the easiest to prepare. Since 1 milliliter of water weighs one gram, we can measure a volume instead of weighing the solvent. A very common use of w/w formulas is with media for the culture of bacteria. Such media come in granular or powdered form, often contain agar, and often require heat in order to dissolve the components. Microbiological media, especially when they contain agar, are difficult to transfer from one vessel to another without leaving material behind. They coat the surfaces of glassware, making quite a mess.

Using a w/w formula the media and water can be mixed, heated, then sterilized, all in a single container. Very little material is wasted and there is less of a mess. By convention, the volume of liquids and gases is often expressed in units of liters or milliliters, measured with glassware. The dimensions of regularly shaped solids can be measured directly with rulers or calipers, which have linear units, giving volumes in units such as cubic centimeters. One milliliter is equivalent to one cubic centimeter. Most solid substances are irregularly shaped, which complicates volume determination.

It is inaccurate, for example, to determine the volume of a powder by measuring its dimensions. A graduated cylinder containing a known volume of liquid is tared. The solid is added to the cylinder, and the total mass is weighed again to determine the mass of the solid. Addition of the solid causes an upward displacement of the liquid, resulting in a new volume reading. The volume of the solid is equal to the change in volume due to liquid displacement (i.e., the difference in liquid volume before and after adding solid).

Measuring the volume depends on your object's state of matter. For liquids, you can use a graduated cylinder or burette for the chemistry lab measurements, or a measuring cup & spoon for everyday life purposes. For gases, to roughly measure the volume, you can inflate a balloon and use it to displace the water in a graduate cylinder. A similar method works for solids — put the object into a graduated container and measure the change in reading. An aqueous solution consists of at least two components, the solvent and the solute .

Usually one wants to keep track of the amount of the solute dissolved in the solution. One could do by keeping track of the concentration by determining the mass of each component, but it is usually easier to measure liquids by volume instead of mass. Molarity is defined as the number of moles of solute divided by the volume of the solution in liters. Table 1 lists results for the determination of the density of ethanol using a 50-mL volumetric flask. Densities were calculated by dividing the measured mass by 50.0 mL.

Table 2 lists results for the determination of the density of a sample of zinc metal using a 100-mL graduated cylinder and the liquid displacement method. Note that the measured densities are constant for both substances. Table 2, in particular, demonstrates that density is independent of the amount of substance studied.

For regular three-dimensional objects, you can easily calculate the volume by taking measurements of its dimensions and applying the appropriate volume equation. If it's an irregular shape, you can try to do the very thing that caused Archimedes to shout the famous word Eureka! Probably you heard that story - Archimedes was asked to find out if the Hiero's crown is made from pure gold or just gold-plated - but without bending or destroying it. The idea came to him when he was taking a bath - stepping into a bathtub, he noticed that the water level rose. From this observation, he deduced that volume of water displaced must be equal to the volume of the part of his body he had submerged.

Knowing the irregular object volume and its weight, he could calculate the density and compare it with the density of pure gold. Legend says that Archimedes was so excited about this discovery that he popped out of his bathtub and ran naked through the streets of Syracuse. When we describe a concentration as a percentage without specifying the type of formula, we imply that the solution is to be made using the weight-in-volume (w/v) method. As with w/w, weight-in-volume is a simple type of formula for describing the preparation of a solution of solid material in a liquid solvent.

Suppose that someone has already worked out the details, so all that you have to do is read a formula and make a solution. We can usually assume that a solution is to be aqueous unless stated otherwise. What about the concentration of the substance to be added? Common ways of describing the concentrations of solutions are weight-in-weight, weight-in-volume, volume-in-volume, and molarity. Less commonly used descriptions include normality and molality. A quantity of solute is measured out, mixed with solvent, and the volume is brought to some final quantity after the solute is completely dissolved.

That is, solutions are typically prepared volumetrically. Because solutes add volume to a quantity of solvent, this method of preparation of solutions is necessary to ensure that an exact desired concentration is obtained. This demonstration illustrates the methods for measuring the density of solids and liquids. Using a volumetric flask and an analytical balance, the density of ethanol can be determined.